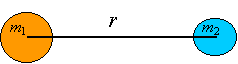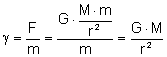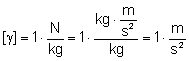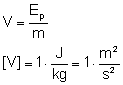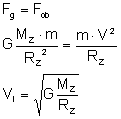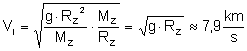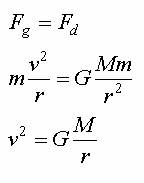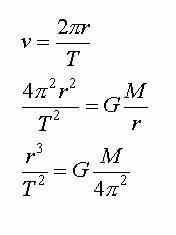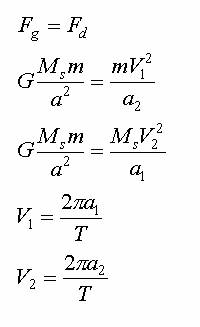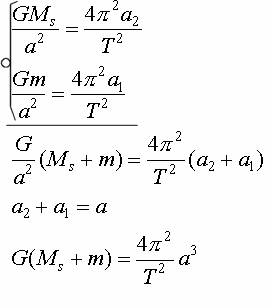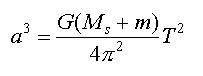GRAWITACJA
Zjawisko grawitacji jest
spoiwem Wszechświata - jest podstawową siłą działającą pomiędzy dużymi
ciałami - w szczególności ciałami niebieskimi. Jest siłą powszechną, obecną w
dowolnym zakątku kosmosu.
Jednak w naszym typowym
ludzkim otoczeniu siła ta jest dostrzegana wyłącznie jako przyciąganie
otaczających nas przedmiotów przez ziemski glob, czyli przez zjawisko ciężaru.
Wzór Newtona na siłę grawitacji
Wzór Newtona na siłę
grawitacji obowiązuje dla dowolnych ciał obdarzonych masą.
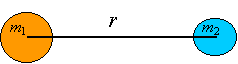
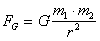
m1, m2
- masy oddziaływujących grawitacyjnie ciał
r - odległość między środkami ciał
G - stała grawitacji, G = 6.67·10-11Nm2/kg2.
Słowne sformułowanie prawa grawitacji
powszechnej
Siła grawitacji
działająca między dwoma ciałami jest wprost proporcjonalna do iloczynu mas
oddziaływujących ciał i odwrotnie proporcjonalna do kwadratu odległości
między ich środkami.
Uwagi
do wzoru na siłę grawitacji
Opisywana postać wzoru
(prawa) odnosi się do dwóch ciał punktowych lub kulistych (ściślej o tzw. kulistosymetrycznym rozkładzie masy).
Prawo grawitacji Newtona jest prawem przybliżonym - dla bardzo dużych mas i
małych odległości między nimi może ujawnić się odchylenie od opisywanego
wzoru. Przewiduje to ogólna teoria względności Einsteina.
Do omawianego wzoru stosuje
się oczywiście 3 zasada dynamiki Newtona, co oznacza, że oba ciała się
przyciągają tą samą siłą. Dlatego nie ma sensu pytać o to, czy to lżejsze
ciało "bardziej" przyciąga cięższe, czy odwrotnie...
Wektorowa postać
wzoru na siłę grawitacji
Wektorowa postać wzoru
oprócz informacji o wartości siły grawitacji przekazuje również dane o
kierunku tej siły.
Przedstawiony poniżej wzór
opisuje sytuację, w której środek układu współrzędnych znajduje się w jednej
z mas podlegających oddziaływaniu.
Od wzoru skalarnego różni się on dodatkiem "kierunkowym" (iloraz
wektora wodzącego przez długość tego wektora) oraz znakiem minus.
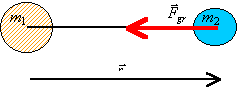
Na powyższym rysunku wektor
wodzący  został przeniesiony pod rysunek kulek
symbolizujących masy. Wynika to wyłącznie z wymogów czytelności, gdyż typową
sytuacją byłoby umieszczenie wektora wodzącego na tej samej linii, co wektora
siły grawitacji Fgr . został przeniesiony pod rysunek kulek
symbolizujących masy. Wynika to wyłącznie z wymogów czytelności, gdyż typową
sytuacją byłoby umieszczenie wektora wodzącego na tej samej linii, co wektora
siły grawitacji Fgr .
Wektorowa postać wzoru
oprócz informacji o wartości siły grawitacji przekazuje również dane o
kierunku tej siły. Wzór poniższy opisuje sytuację, w której środek układu
współrzędnych znajduje się w jednej z mas podlegających oddziaływaniu.
Od wzoru skalarnego różni się on dodatkiem "kierunkowym" (iloraz
wektora wodzącego przez długość tego wektora) oraz znakiem minus.
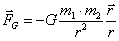
W tym wzorze minus związany
jest faktem, że siła działa przeciwnie do zwrotu promienia wodzącego.
Natężenie pola grawitacyjnego
Wyobraźmy sobie przestrzeń w kosmosie oddaloną od wszelkich ciał. Jeżeli w
punkcie tej przestrzenie umieścimy masę próbną, to zgodnie z przewidywaniami
nie będzie działać na niego żadna siła. Jeżeli zaś umieścimy tę masę próbną
blisko jakiegoś obiektu, np. planety, to na ciało
oczywiście będzie działać siła. Przy czym siła ta nie jest wywołana
bezpośrednim kontaktem planety i tej masy próbnej. Planeta oddziaływuje na niego "na odległość".
Mówimy, że ciało (w naszym przykładzie planeta) o masie "M"
wytwarza pole grawitacyjne, które zmienia właściwości przestrzeni wokół
siebie w ten sposób, że jeżeli w tym polu umieścimy ciało o masie
"m" to zadziała na nie siła określona prawem ciążenia.
Polem grawitacyjnym nazywamy więc własności
przestrzeni, które informują nas jaka siła będzie działać na ciało
"m" kiedy je tam umieścimy. Z takiego rozumowania uzyskujemy zależność:
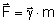
Patrząc na tę wielkość z
innej strony możemy powiedzieć, że natężenie pola grawitacyjnego w danym
punkcie przestrzeni jest równe liczbowo wartości siły grawitacyjnej
działającej na ciało o masie 1
kg umieszczone w tym punkcie.
Zobaczmy jakim wzorem wyraża się natężenie pola
grawitacyjnego i jaka jest jego jednostka:
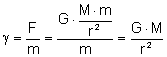
Jednostka natężenia pola:
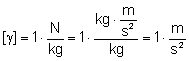
Widzimy, że jednostka jest
taka sama jak jednostka przyśpieszenia. Okazuje się, że wartość natężenia
pola w danym punkcie przestrzeni równa jest liczbowo także przyśpieszeniu grawitacyjnemu jakie uzyska to ciało po umieszczeniu go w
tym punkcie przestrzeni.
Z tej własności wiemy jaki jest natężenie pola
grawitacyjnego przy powierzchni Ziemi:
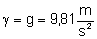
Linie pola grawitacyjnego
W naszych rozważaniach używamy zwykle dwóch rodzajów pól grawitacyjnych:
jednorodnych i centalnych. Omawiając pola niesposób niewspomnieć o
liniach pola. Są to kierunki do których styczne są
wektory sił grawitacyjnych. Przy powierzchni Ziemi mamy do czynienia z
jednorodnym polem grawitacyjnym. Na każde ciało które posiada masę działa siła,
której wektor ma kierunek pionowy. Więc wszystkie linie pola grawitacyjnego
przy powierzchni Ziemi wyznaczają pion.
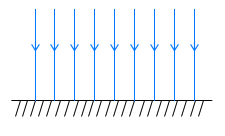
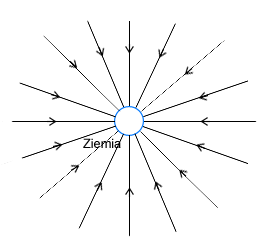
Ale jeżeli patrzymy na
Ziemię z daleka lub traktujemy ją jako punkt materialny, to zauważymy że wektor siły działającej na ciało znajdujące
się nad biegunem będzie prostopadły do wekora siły
działającej na ciało znajdujące się nad równikiem. Jeżeli narysujemy wiele
takich linii to uzyskamy efekt promienii
rozchodzących się ze Słońca. W środku źródło pola grawitacyjnego, a dookoła
niego promieniście rozłożone linie tego pola.
Praca w polu grawitacyjnym
Wykonajmy pewne doświadczenie myślowe. Zadaniem tego doświadczenia będzie
wykonanie pracy polegającej na przemieszczeniu ciała z punktu A do punktu B, przy czym oba punkty znajdują się w jednym
pionie ale na różnych wysokościach (punkt A leży pod punktem B). Krótko
mówiąc będziemy podnosić ciało i obliczymy pracę. Ciało przemieszczamy ruchem
jednostajnym prostoliniowym, a siła jaką działamy
równa jest co do wartości sile grawitacji. W miarę zwiększania wysokości siła
ta jest coraz mniejsza. Więc siła jaką działamy na
początku (w punkcie A) jest większa od tej której używamy na końcu drogi (w
punkcie B). Siła maleje odwrotnie proporcjonalnie do kwadratu odległości więc
wyliczając średnią siłę posłużyć się musimy tzw. średnią geometryczną:
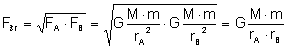
Gdzie:
FA - siła działająca w punkcie A
FB - siła działająca w punkcie B
rA i rB - odległość od źródła pola grawitacyjnego
punktów A i B
M - masa źródła pola grawitacyjnego
m - masa ciała nad którym wykonujemy pracę.
Obliczmy zatem wykonaną pracę:
α - kąt między wektorem średniej siły a wektorem przesunięcia
Zauważmy, że kąt α=0° więc cos(α)=1, gdybyśmy ciało opuszczali z
punktu B do punktu A to α=180° a cos(α)=-1, więc praca miała by
wartość ujemną. Uniwersalny wzór, niezależnie od tego czy opuszczamy ciało,
czy podnosimy wygląda następująco:
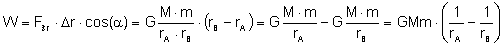
Praca jest dodatnia jeżeli ciało podnosimy, a ujemna jeżeli ciało
opuszczamy.
Z ostatniego wzoru wynika, że praca nie zależy od drogi po
jakiej poruszało się ciało gdy wykonywaliśmy pracę nad nim. Zależy
jedynie od punktu początkowego i końcowego. Jeżeli ciało przebędzie drogę Δr po prostej lub "na około" to praca
będzie taka sama. Takie pole w którym praca nie
zależy od drogi, a jedynie od położenia początkowego i końcowego ciała
nazywamy polem zachowawczym.
Energia potencjalna w polu
grawitacyjnym
W poprzednich tematach liczyliśmy energię potencjalną ciała znajdującego się
na pewnej wysokości, ale stosunkowo blisko powierzchni Ziemi. W takiej
sytuacji siłę działająca na ciało można uznać za stałą (nie
zmieniającą się wraz z wysokością). Jeżeli jednak rozpatrujemy duże
wysokości, to już nie możemy tak uprościć rozważań. Siła zmienia się wraz z
wysokością, więc i energię potencjalną musimy liczyć w inny sposób.
Wiemy, że energia równa jest wykonanej pracy nad ciałem. Jeżeli wykonamy taką
pracę i przemieścimy ciało z miejsca gdzie nie ma ono energii potencjalnej do
miejsca gdzie tę energię ma, to praca jaką wykonamy
będzie równa tej energii. Zastanówmy się gdzie w przestrzeni ciało nie ma
energii potencjalnej? Jeżeli oddalimy ciało od źródła pola grawitacyjnego tak dlatego, że nie będzie na niego działała żadna siła ze
strony tego źródła to w tym miejscu nie będzie to ciało mieć energii
potencjalnej.
Przenieśmy więc ciało z bardzo daleka (z
nieskończoności) do punktu oddalonego o r od źródła
pola grawitacyjnego. Ciało to będzie się zbliżać do źródła. Pamiętamy z
poprzedniego paragrafu, że jeżeli ciało opuszczamy (zbliżamy do źródła) to praca jaką wykonujemy ma wartość ujemną. Więc nasza
energia potencjalna będzie miała wartość ujemną:
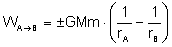
Energia
potencjalna jest więc ujemna. A oznacza to, że prace
wykonuje siła przyciągania, a nie jak w poprzednich przypadkach siła która równoważyła siłę przyciągania.
Potencjał grawitacyjny
Omówiliśmy już taką wielkość jak natężenie pola grawitacyjnego, która mówi
nam jak silne jest pole wytworzone przez dane źródło. Wartość natężenia
informowała nas o sile jaka zadziała na jednostkową
masę (np. 1 kg) umieszczoną w danym punkcie pola. Jest
jeszcze inna wielkość fizyczna która charakteryzuje
pole grawitacyjne. Jest nią potencjał grawitacyjny. Ta wielkość informuje nas jaka będzie energia potencjalna ciała o jednostkowej
masie (np. 1 kg) umieszczonego w danym punkcie tego
pola. Potencjał wyraża się wzorem:
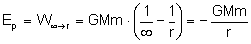
Sprawdźmy
od czego zależy potencjał grawitacyjny. W tym celu
rozwińmy nasz wzór:
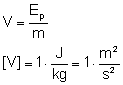
Jak widać potencjał nie
zależy od masy ciała umieszczonego w polu grawitacyjnym, lecz od masy źródła
i odległości od niego.
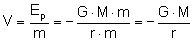
Znając potencjał
grawitacyjny w punktach A i B łatwo możemy obliczyć pracę
jaką należy wykonać by ciało o masie "m" przemieścić z
jednego punktu do drugiego:
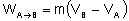
Pierwsza prędkość kosmiczna
W XX w. nastąpił wielki przełom w dziejach
ludzkości. Otóż udało się człowiekowi opuścić Ziemię i udać się do kosmosu.
Lecz takie czynności stwarzają nowe zadania dla fizyków. Potrzebne stało się liczenie jakie prędkości należy nadać rakiecie żeby
wystartowała i wyniosła statek na orbitę, albo by dolecieć do Księżyca. Jedna
z takich charakterystycznych prędkości została nazwana pierwszą prędkością
kosmiczną i mówi nam jak szybko musi poruszać się ciało, by mogło lotem
bezsilnikowym okrążyć Ziemię po orbicie tuż przy jej powierzchni. Jest to
najmniejsza możliwa prędkość jaką może mieć sztuczny
satelita Ziemi. Ale w rzeczywistości satelity znajdują się dużo wyżej nad
powierzchnią ok. 160 km
nad Ziemią, bo poniżej tej wysokości występują opory powietrza.
Siła ciężkości jaka działa na ciało musi być
zrównoważona. W nieinercjalnym układzie odniesienia
tą równoważącą siłą jest odśrodkowa siła bezwładności więc:
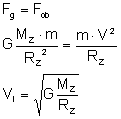
Gdzie MZ i RZ
to masa i promień Ziemi. Jeżeli ze wzoru na
natężenie pola grawitacyjnego wyliczymy G to otrzymamy:
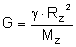
Tę wartość możemy teraz
podstawić do wzoru na pierwszą prędkość kosmiczną. Skorzystajmy jeszcze z
własności natężenia pola grawitacyjnego która mówi,
że jest ma ona taką samą wartość jak przyśpieszenie grawitacyjne (przy
powierzchni ziemi równe "g").
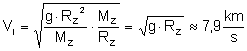
Druga prędkość kosmiczna
Ta prędkość informuje nas jak musimy rozpędzić statek kosmiczny
aby opuścił pole grawitacyjne Ziemi i udał się w nieskończoność.
Jeżeli ciało zostanie wyrzucone z Ziemi z prędkością większą od pierwszej a
mniejszą od drugiej prędkości kosmicznej to jej ruch będzie następujący:
statek poruszać się będzie w przestrzeń kosmiczną z prędkością coraz
mniejszą, aż do momentu gdy siły grawitacyjne Ziemi
zatrzymają ten statek. Następnie te siły nadadzą przyśpieszenie skierowane w
stronę Ziemi i w ten sposób statek zawróci. Tor po jakim
będzie się poruszał będzie elipsą.
Jeżeli zaś statek wyrzucimy z Ziemi z drugą prędkością kosmiczną to siły
grawitacyjne będą powodować zmniejszenie prędkości statku a w nieskończoności
go zatrzymają, lecz nie zdołają go zawrócić. Jeżeli prędkość początkowa będzie choć trochę większa od drugiej prędkości kosmicznej
to ciało nie zatrzyma się.
Wyliczając drugą prędkość kosmiczną posłużymy się własnością, że całkowita
energia mechaniczna ciała w nieskończoności równa jest zeru. Energia
kinetyczna równa jest zeru ponieważ ciało się w
nieskończoności zatrzyma. Także energia potencjalna będzie równa zero, co
wynika bezpośrednio ze wzoru.
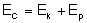
Na początku energia statku
wynosi:
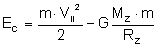
W nieskończoności:

Łatwo zauważyć
że:
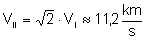
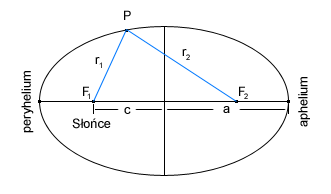
Pierwsze prawo Keplera
Planety krążą po orbitach eliptycznych, a jednym z ognisk elipsy jest Słońce
Drugie prawo Keplera
Pola powierzchni wycinków elipsy zakreślone przez promień wodzący planety w
jednakowych przedziałach czasu są jednakowe.
Prawo to obrazuje rysunek:
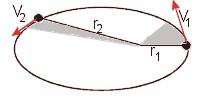
Zgodnie z II prawem
Keplera, zaznaczone na szaro pola są równe. Wynika z tego, że prędkość V2jest
mniejsza niż V1
Trzecie prawo Keplera
Dla każdej planety Układu Słonecznego stosunek sześcianu średniej odległości
od Słońca do kwadratu okresu obiegu wokół tej gwiazdy jest stały.
Brzmi to może troszeczkę
skomplikowanie, ale myślę, że wszystko wyjaśni się, jeśli to prawo
wyprowadzimy.
Rozpatrujemy planetę, która porusza się w polu grawitacyjnym Słońca: m - masa
tej planety
M - masa Słońca
r - odległość tej planety od Słońca
T - okres obiegu planety wokół Słońca
zakładamy, ze planeta porusza się po okręgu, zatem siła dośrodkowa jest równa
sile oddziaływania grawitacyjnego między tymi planetami:
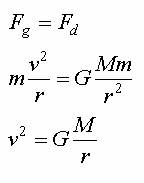
Z ruchu po okręgu możemy
obliczyć prędkość:
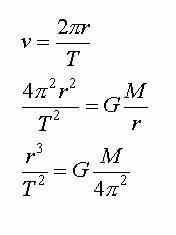
Otrzymaliśmy
więc III prawo Keplera ponieważ G,M
są stałe, zatem stosunek sześcianu promienia do kwadratu okresu obiegu jest
stały. Jest to tak zwane nieuogólnione III prawo
Keplera.
Teraz zagadnienie nico trudniejsze, wyprowadzimy uogólnione III prawo
Keplera. Będzie tu trochę więcej matematycznych przekształceń i kilka
ciekawych pojęć fizycznych.
Zakładamy, że planeta o masie m i gwiazda o masie M krążą wokół
ich wspólnego środka masy O tak jak na rysunku:
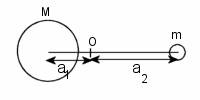
a =
a1 + a2 - odległość między planetą, a gwiazdą
v1 - prędkość liniowa gwiazdy
v2 - prędkość liniowa planety
T - okres obiegu planet wokół ich wspólnego środka masy.
Wiemy, że w obudwu przypadkach siła dośrodkowa jest równa sile
grawitacji, prędkość można wyznaczyć z ruchu po okręgu, a plantey
poruszają się po orbitach o promianiach a1
i a2:
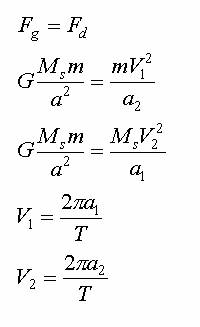
Po odpowiednim podstawieniu
i skróceniu otrzymujemy układ równań, który następnie dodajemy stronami:
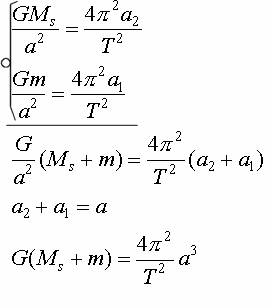
Po odpowiednim
przekształceniu otrzymujemy III prawo Keplera uogólnione
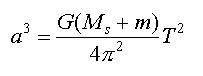
Z uogólnionego III prawa
Keplera bardzo łatwo wyprowadzić prawo nieuogólnione,
wystarczy zapisać uogólnione prawo dla 2 planet, a następnie podzielić
stronami. Następnie założyć, że masy planet względem masy Słońca są
pomijalnie małe i otrzymać:

|